Projectile Range Calculator
Calculate the horizontal distance traveled by a projectile
Determine projectile range using velocity, launch angle, and initial height with LRU bidirectional solving and multiple unit systems.
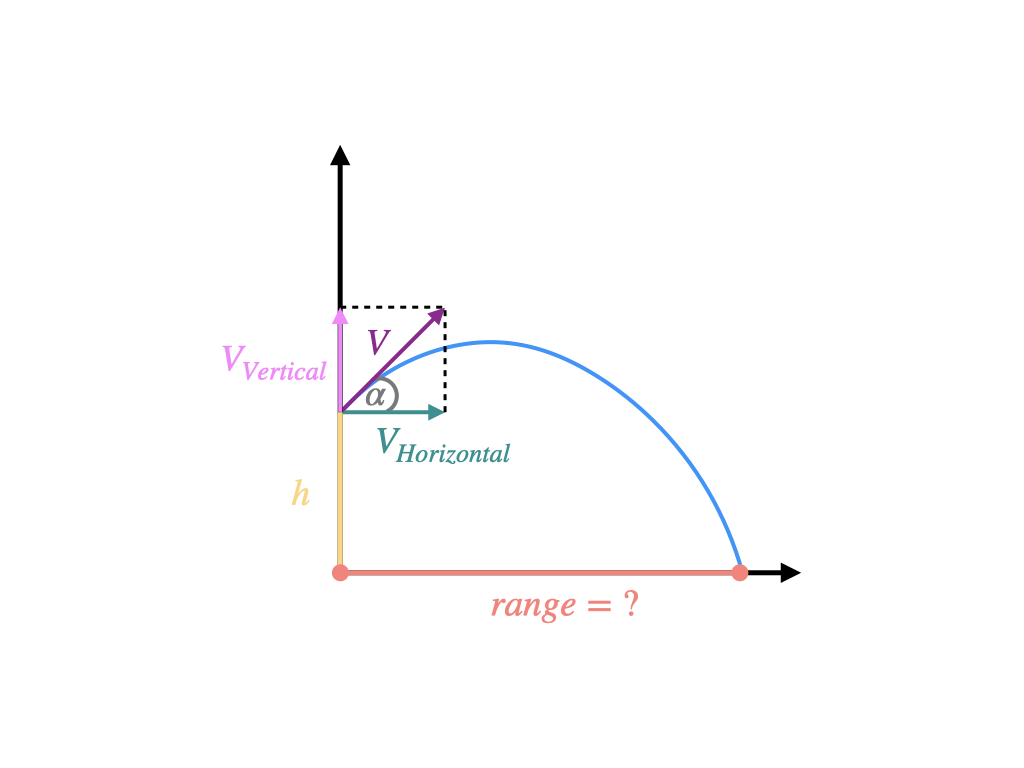
What is the Projectile Range Calculator?
The Projectile Range Calculator is a specialized tool designed to determine the horizontal distance an object travels when launched into the air. By accounting for initial velocity, launch angle, and starting height, it provides an accurate prediction of where an object will land.
This tool is essential for anyone dealing with motion in two dimensions. Whether you're calculating the path of a football, a volcanic rock, or a scientific experiment, this calculator simplifies complex physics into instant results.
💡 Pro Tip: For a more comprehensive analysis including flight time and maximum height, try our Projectile Motion Calculator.
Quick Start Guide
Enter the Initial Velocity (how fast the object is moving at the start).
Input the Launch Angle (the angle relative to the ground).
Specify the Initial Height (if launching from a platform or building).
The Range will be calculated automatically in real-time!
Example Calculation
Imagine a rock ejected from a volcano:
- Velocity: 30 m/s
- Angle: 25°
- Height: 100 m (launching from a peak)
Resulting Range
162.87 meters
Real-World Use Cases
The Football Kick
A player kicks a ball from the ground at 22 m/s at a 35° angle.
Basketball Shot
A 2m tall player shoots at 8.2 m/s with a 45° angle.
Volcanic Eruption
Lava rocks ejected at high speeds from a mountain peak.
When to Use This Calculator
- ✅
Physics Education
Perfect for verifying homework answers or visualizing how changing an angle affects the landing spot.
- ✅
Sports Optimization
Athletes in shot put, javelin, or long jump can use these principles to find their "ideal" launch angle.
- ❌
High-Speed Ballistics
For bullets or long-range missiles, air resistance (drag) becomes a major factor that this basic model does not include.
Tips for Accuracy
The 45-Degree Rule
On flat ground, a 45° angle always provides the maximum range. If you're launching from a height, the optimal angle is actually slightly less than 45°!
Mind the Units
Ensure your velocity is in m/s and height is in meters for the most standard results. Our calculator handles the conversions for you if you prefer feet or mph.
The Physics Behind the Range
1. Launch from Ground Level (h = 0)
When the starting and ending heights are the same, the formula is elegant and simple:
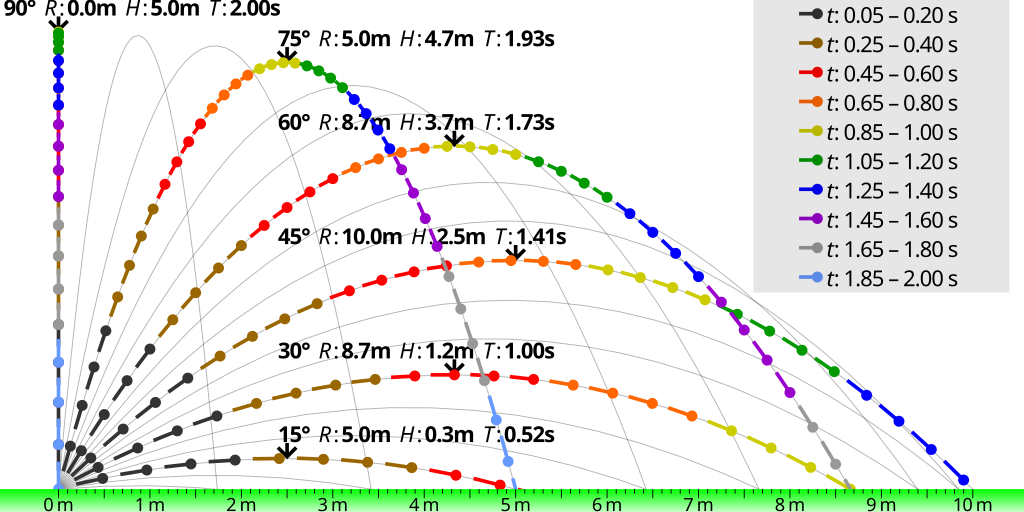
Visualizing Angle Impact on Range and Height
This scientific visualization demonstrates how the launch angle dictates the parabolic path when objects are launched at the same initial speed under a constant gravity field (g = 10 m/s²). Notice how 45° yields the maximum horizontal distance (R), while steeper angles increase the peak height (H). The markers represent 0.05-second intervals, with the "tails" indicating instantaneous velocity.
2. Launch from an Elevation (h > 0)
When launching from a height, the object stays in the air longer, requiring a more complex equation:
Frequently Asked Questions
What exactly is 'range' in projectile motion?
Range is the total horizontal distance an object travels from its launch point to the point where it returns to the same vertical level (or hits the ground). It's purely the 'forward' distance, ignoring the height of the arc.
Does the mass of the object affect the range?
In a vacuum (no air resistance), no! A bowling ball and a marble launched at the same speed and angle will land in the exact same spot. In the real world, mass only matters because it helps overcome air resistance.
Why is 45 degrees the best angle for distance?
Mathematically, the range formula uses sin(2α). The sine function reaches its maximum value (1) at 90 degrees. Since we use 2α, 45 degrees (2 * 45 = 90) gives us that maximum value.
Can I calculate range if I only have horizontal speed?
Yes! If you launch horizontally (angle = 0), the range depends entirely on your height. You can use this calculator by setting the angle to 0, or check out our specific Horizontal Projectile Motion Calculator.
What is the 'minimum' range possible?
The minimum range is zero, which happens if you fire the object straight up (90°) or straight down. In both cases, the object has no horizontal velocity component.
Limitations & Disclaimers
Note: This calculator assumes "ideal" projectile motion. It does not account for air resistance, wind speed, or the curvature of the Earth. In real-world conditions, objects will typically travel slightly less distance than calculated here due to drag. This tool is for educational and recreational purposes and should not be used for critical engineering or safety-related ballistics.
External References / Sources
- Galilei, G. (1638). Two New Sciences. Leiden. p. 249.
- Stewart, J., Clegg, D., & Watson, S. (2021). Calculus: Early Transcendentals (9th ed.). Cengage. p. 919. ISBN 978-1-337-61392-7.
- Tatum. (2019). Classical Mechanics (Chapter 7) [PDF].
- Thornton, S. T., & Marion, J. B. (2007). Classical Dynamics of Particles and Systems. Brooks/Cole. p. 59. ISBN 978-0-495-55610-7.
Related Calculators
Trajectory Calculator
Have a look at the flight path of the object with this trajectory calculator.
Free Fall Calculator
Calculate free fall parameters including gravitational acceleration, drop height, fall duration, and impact velocity. Supports bidirectional LRU solving with unit conversions.
Free Fall with Air Resistance Calculator
Calculate free fall with quadratic air drag, including terminal velocity, fall time, maximum velocity, and drag force. Supports air resistance coefficient calculation from object properties.
Projectile Motion Calculator
Calculate projectile trajectory parameters including launch velocity, angle, distance, maximum height, and flight time with bidirectional solving.
Maximum Height Calculator – Projectile Motion
Use this maximum height calculator to figure out what is the maximum vertical position of an object in projectile motion.
Time of Flight Calculator – Projectile Motion
Check out how long a projectile remains in the air with this time of flight calculator.